SVG Learning - 2

SVG 学习第二部分，包括<path>图形元素。简单罗列，英文为主。

References

• An SVG Primer for Today’s Browsers
  • Copyright © 2010 W3C® (MIT, ERCIM, Keio), All Rights Reserved.

SVG graphics elements

• <path>
• <line>
• <rect>
• <circle>
• <line>
• <polyline>
• <polygon>
• <image>
• <use>

<path>

M & L

• M x y: Move pen to (x, y)
• M x1,y1[ x2,y2[…]]: Move pen to (x1, y1), then (x2, y2), …
• M x1 y1 L x2 y2[ x3 y3[…]], M x1 y1 L x2,y2[ x3,y3[…]]: Draw linearly from (x1, y1) to (x2, y2), then (x3, y3), …

SVG Code

<path stroke="black" d="M 100 100 L 200 200"/>

Illustration

A diagonal line from (100,100) to (200,200)

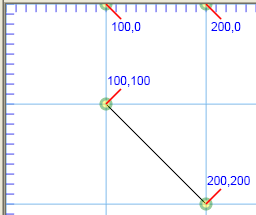
SVG Code

<path d="M 100 100 L 200 200 100 150"/>

Illustration

Concatenated pairs of coordinates

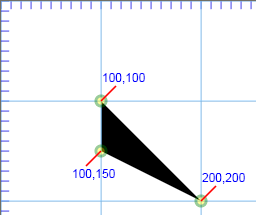
SVG Code

<path d="M 50,100 150,200 50,150"/>

<path d="M 100 50 L 200 150 100 100" fill="none" stroke="black"/>

The effect of adding fill="none" (but note that the stroke attribute is defined)

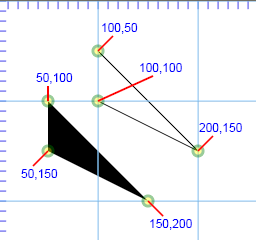
• z: Close path

SVG Code

<path d="M 100,50 200,150 100,100" fill="none" stroke="black"/>

<path d="M 100,50 200,150 100,100 z" fill="none" stroke="black"/>

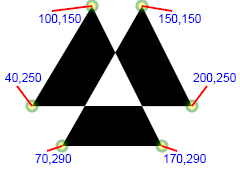
fill-rule="even-odd"

SVG Code

<path d="M 70,290 L 150,150 200,250 40,250 100,150 170,290"/>

<path d="M 70,290 L 150,150 200,250 40,250 100,150 170,290" fill-rule="evenodd"/>

An example to show the difference between the default and "even-odd" fill rules

An example to show the difference between the default and "even-odd" fill rules

Combine multiple path segments

SVG Code

<path fill="orange"
    d="M 10,215 210,215 110,42 z
    M 10,100 210,100 110,273 z"
    stroke="purple" stroke-width="3"/>

A \<path\> with fill="green" et cetera... is also included in the drawing.

Q: Quadratic Bézier curves

• M x1 y1 Q x2,y2 x3,y3: Draw quadratically from (x1, y1), then (x2, y2), towards (x3, y3)

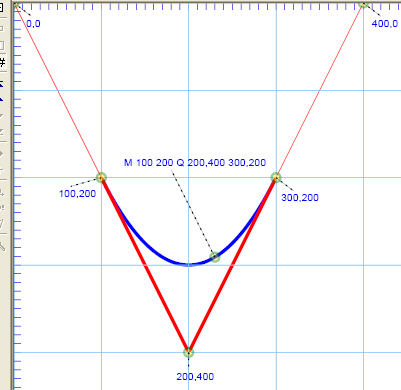
SVG Code

<path d="M 100 200 Q 200,400 300,200" fill="none" stroke="blue" />

<path d="M 100 200 L 200,400 300,200" fill="none" stroke="red"/>

Illustration

Bézier curve example

SVG Code

<path fill-rule="evenodd"
    d="M 70 140 L 150,0 200,100 L 40,100 100,0 L 170,140 70 140"/>

<path fill="red" fill-rule="evenodd"
    d="M 70 140 Q 150,0 200,100 Q 40,100 100,0 Q 170,140 70 140"/>

Illustration

An example of a graphic using a quadratic spline

C: Cubic Bézier curves

• M x1 y1 C xt1,yt1[ xt2,yt2[…]] x2,y2: Draw cubically from (x1, y1) to (x2, y2), with control points (xt1, yt1), (xt2, yt2), …

A family of cubic curves sharing endpoints and tangents

Limiting case for a family of curves

Cubic beziers sharing tangents and endpoints

Adjoining two cubic curves smoothly

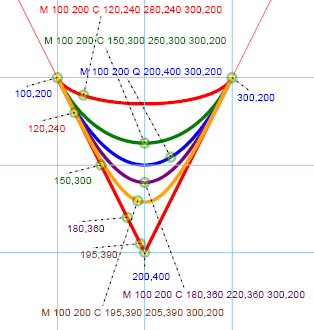
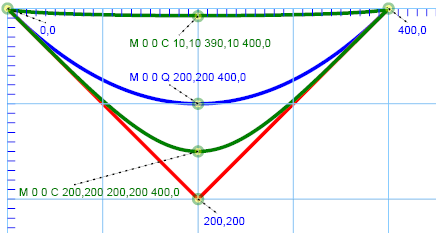
SVG Code

<path stroke="black" stroke-width="3" fill="#eec1c2"
d="M 99 192
C 137 160 204 133 141 124
C 78 115 34 167 47 129
C 60 91 20 65 77 71
C 134 77 206 43 196 101
C 186 159 118 368 119 299
C 120 230 201 169 138 206
C 75 243 53 231 99 192" />

Illustration

Several smoothly stitched Bézier segments

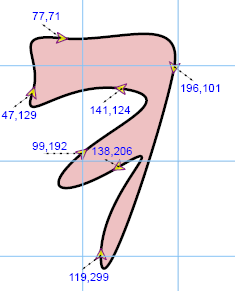
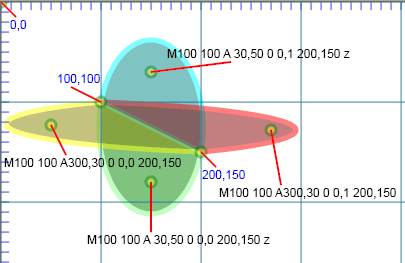
A: Elliptical arc

Four elliptical arcs sharing endpoints